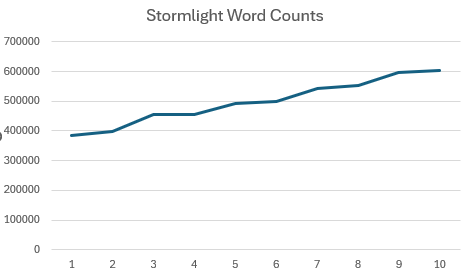
My brother-in-law likes the Brandon Sanderson “Stormlight Archive” series. In our discord he posted about the increasing word count of each book (below), extrapolating to potential books (my mother-in law said “ok, since I know you’ve done it, linear regression extrapolation to Stormlight 25?“)
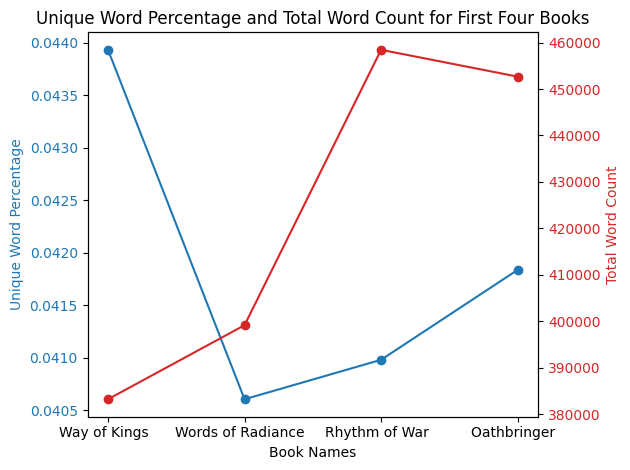
Fantasy/sci-fi books usually have a lot of invented nouns/proper nouns. So then it got me thinking: how many of those words are new within a book? In a series, even though the books get longer, there’s probably some repetition of the words to immerse the reader in the universe, right?
When we plot total word count against the percent of unique words in each, we see that the first book has the highest percent of unique words per word count! So, in a way, though it is the shortest, it is the most informationally dense… Hmmmm… information… bookmarking that.
The graph below shows these values compared to William Faulkner’s The Sound and the Fury, David Foster Wallace’s Infinite Jest, and Thomas Pynchon’s Gravity’s Rainbow—I just grabbed IJ and GR because I think of them as postmodernist books that made me feel like an inadequate reader at times because of their density… Risa (my future sister-in-law) suggested I add the Faulkner. The Faulkner has fewer words, but uses a higher proportion of unique words. Infinite Jest is long (oh wow), but still has a higher percentage of unique words. And, lastly, GR has the highest proportion of unique words.
Reviving the line of thought on information: these results got me thinking about information and entropy: entropy is a quantification of the randomness of the outcomes. Its calculated as The higher the entropy, the more chaotic the outcomes: for example a dice roll is totally random, so its entropy value will be high. Let’s use a die to walk through entropy. The probability of any side is .167. So we calculate the right part of the equation as . We sum all possible outcomes—in this case, the 6 outcomes all have the same probability (a uniform distribution)—and get .
Entropy is relative to the number of outcomes: its possible that certain systems can have higher entropy values because there are a higher number of outcomes. So because Infinite Jest has the highest number of words, it has the highest possible entropy value. Normalized entropy makes it so that the range of its output is between 0–1, where 1 means all outcomes are equal (an unpredictable system). All we have to do is divide the entropy by the logarithmically scaled number of outcomes. Where are the total number of outcomes:
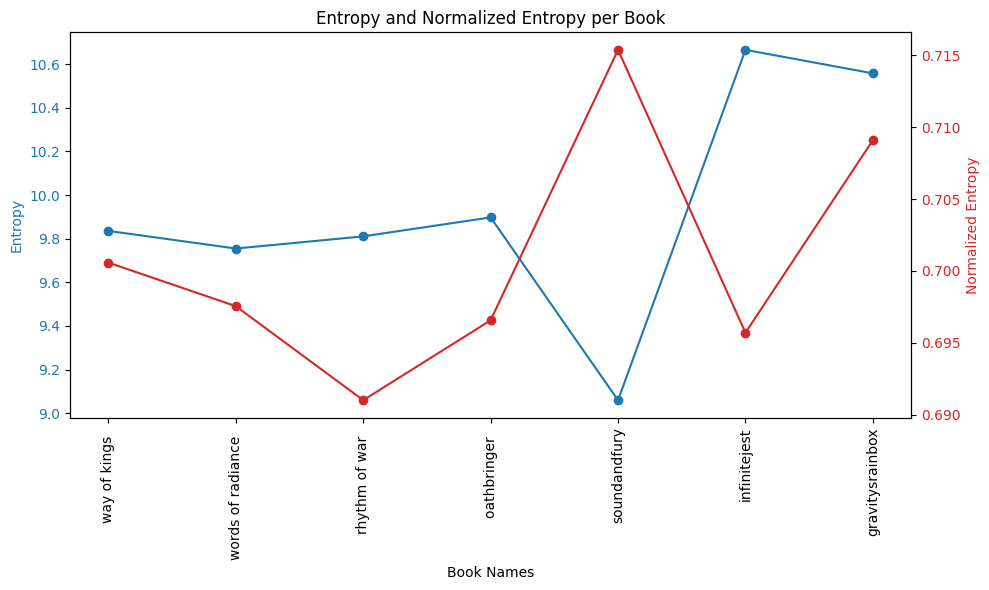
Below are the books with entropy and normalized entropy. I’m going to make a false assumption that entropy corresponds to “density” of the book (i.e. “how dense a read is”), but that is definitely false… Maybe there’s some correlation, but this is a one-day project.
We immediately see the value in normalized entropy: the Faulkner book has the lowest entropy, but the highest normalized entropy; the book has 1/3 the number of words than the other books, but it might be more dense because it has more unique words proportional to those words (shown by the higher normalized entropy value). GR is definitely the book which gives me the most shivers when looking at these charts: its a long book and it has a high normalized entropy value.
Oh yeah, I’ve never read the the Sanderson books… is Rhythm of War the least “dense” out of the Stormlight Archive?
